【题解】[ZqlwMatt 原创题]青蛙 (zby)

发表于 | 分类于 | 误人子弟 个
字数统计: 654 | 阅读时长 ≈ 3

题目背景

ZBY 是一只青蛙！

题目描述

如果一只青蛙在 u (u>1) 号荷叶，他会进行一步等概率的跳跃，从 u 号荷叶跳到 1…u 号荷叶。

现在青蛙在 N 号荷叶，求出他跳到 1 号荷叶的期望步数。

输入输出格式

输入格式：

一个正整数 N 。

输出格式：

答案保留 8 位小数。

输入输出样例

输入样例#1：

2

输出样例#1：

2.00000000

输入样例#2：

3

输出样例#2：

2.50000000

样例解释

第一组数据中，三块碎片两两吻合的方案有 1 种，三块碎片中恰好有一对碎片互相吻合的
方案有 3 种，总共有 4 种方案。

第二组数据中，因为第 1、2 块碎片吻合，第 1、3 块碎片冲突，所以第 2、3 块碎片一定
冲突。

说明

对于 10% 的数据，N ≤ 5

对于 20% 的数据，N ≤ 10000

对于 30% 的数据，N ≤ 1000000

对于 100% 的数据，2 ≤ N ≤ 10^18

解题思路

因为青蛙是 zby，所以
if(n==1) puts(“0.00000000”);
else puts(“1.00000000”);
zbytql!!

感谢北冥咸鱼的倾情讲解。

用 f [ i ] 表示第 i 格到第 1 格的数学期望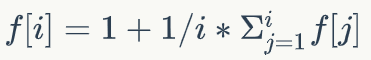
iKqT2V.png

理解一下，然后变形

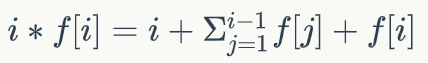
iKqqrF.png

于是可得

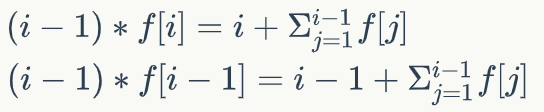
iKqLb4.png

两式相减

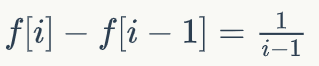
iKqja9.png

就这样得出了优秀的 O( n ) 推导式

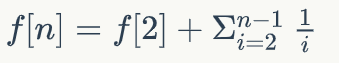
iKqzP1.png

算下调和级数前缀和就知道啦！

就在欣喜之时，我悄咪咪地瞄到了数据范围

…

https://baike.baidu.com/item/%E8%B0%83%E5%92%8C%E7%BA%A7%E6%95%B0/8019971?fr=aladdin

至于为什么较小的点需要用 O( n ) 递推，因为调和级数前缀和公式是无限逼近的…越大的数误差越小，对于 8 位的精度还是稍微保险一点，那个欧拉常数也可以通过暴算打表推出来

嗯，大概就是这样了

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#include <string>
#include <cstdlib>
#include <iostream>
#include <cmath>
#include <set>
#define re register long long
#define rep(i,a,b) for(re i=a;i<=b;++i)
#define drep(i,a,b) for(re i=a;i>=b;--i)
typedef long long ll;
using namespace std;
const int MOD=1000000007;
inline ll read(){
    ll x=0;bool f=0;char ch=getchar();
    while(!isdigit(ch)) f^=!(ch^'-'),ch=getchar();
    while(isdigit(ch)) x=((x+(x<<2))<<1)+(ch^48),ch=getchar();
    return f?-x:x;
}
ll n;
double f[4000010];
int main(){
    n=read();
    if(n<=1000000){
        f[n]=f[2]=2;
        rep(i,2,n-1) f[n]+=1.0/i;
        printf("%.8lf\n",f[n]);
    }
    else printf("%.8lf\n",log(n)+1.5772156649);

    return 0;
}

题目来源

洛谷 U39825 青蛙 (zby)

0%